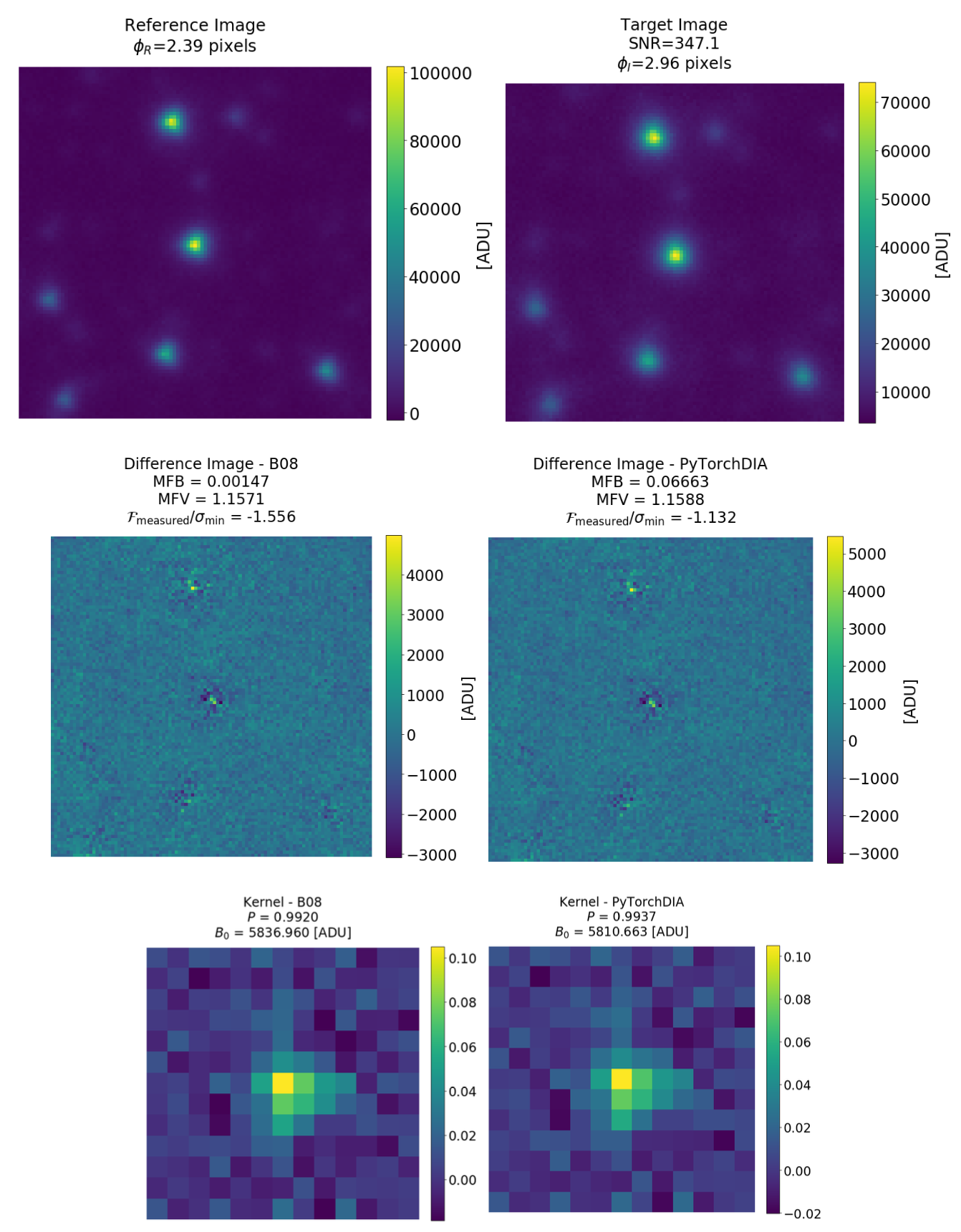
At this week’s meeting I shared an update about a project called PyTorchDIA led by James Hitchcock (St. Andrews) where we are looking into how numerical tools developed for machine learning can be applied to astronomy. Unlike many applications of PyTorch, TensorFlow, etc. in astronomy, I’m not talking about using neural networks. Instead, I’m talking about using PyTorch to compute fast convolutions and matrix-vector products to accelerate more “traditional” astronomy problems. This is somewhat similar in spirit to the wobble project led by Megan Bedell (that strangely has never appeared on this blog, Megan!).
For the PyTorchDIA project, James and I realized that we might be able to easily port existing difference imaging methods to run on the GPU using PyTorch since the bottleneck operation is solving a large linear problem where the design matrix is a convolution. This is exactly the type of operation encountered in deep learning applications and exactly what frameworks like PyTorch are designed for. James took this one step further, and instead of directly solving this linear system, he uses an iterative solver that only requires matrix-vector products (rather than a full Cholesky factorization). This allows us to relax some of the assumptions (like Gaussianity of the observation model) of the standard methods so that we can use a robust loss function instead of sigma clipping.
Using the GPUs available on Google Colab, James finds that his method is at least an order of magnitude faster than optimized implementations of other commonly used methods for difference imaging, across a wide range of realistic test cases. We will hopefully be submitting this paper in the next week or so and we are already planning on incorporating this method into the pipelines for several existing and upcoming difference imaging surveys. But, the real reason why I shared this with the group was that I believe that there are some (potentially) useful lessons learned:
- Astronomical imaging analysis shares a lot of structure with machine learning problems; let’s take advantage of that!
- Some of the linear problems that we work on in the group might be easier and faster to solve if we use iterative solvers rather than direct solvers. The scaling is different, but also the implementations have been optimized for the forward calculation and these methods can open the possibility of generalizing the loss function.
Aside: I also want to mention the awesome website weirdgalaxi.es (yes that is the domain name, but don’t click on that if you’re using Safari) that Kate Storey-Fisher made (and shared at this week’s meeting) as a continuation of the project that she previously blogged about.