With Gaby Contardo (Flatiron), I’m looking at data-mining or discovery methods for point-cloud data. Our current approaches depend on finding and relating critical points (minima, saddle points, maxima) of smooth models of the density field. These smooth models need to be twice differentiable, which is actually a pretty hard criterion: It means that we can’t use many of the standard kernels in kernel-density estimation (KDE), and we can’t use certain kinds of common speed-ups for KDE, because most speed-ups make the density estimates (technically) non-continuous.
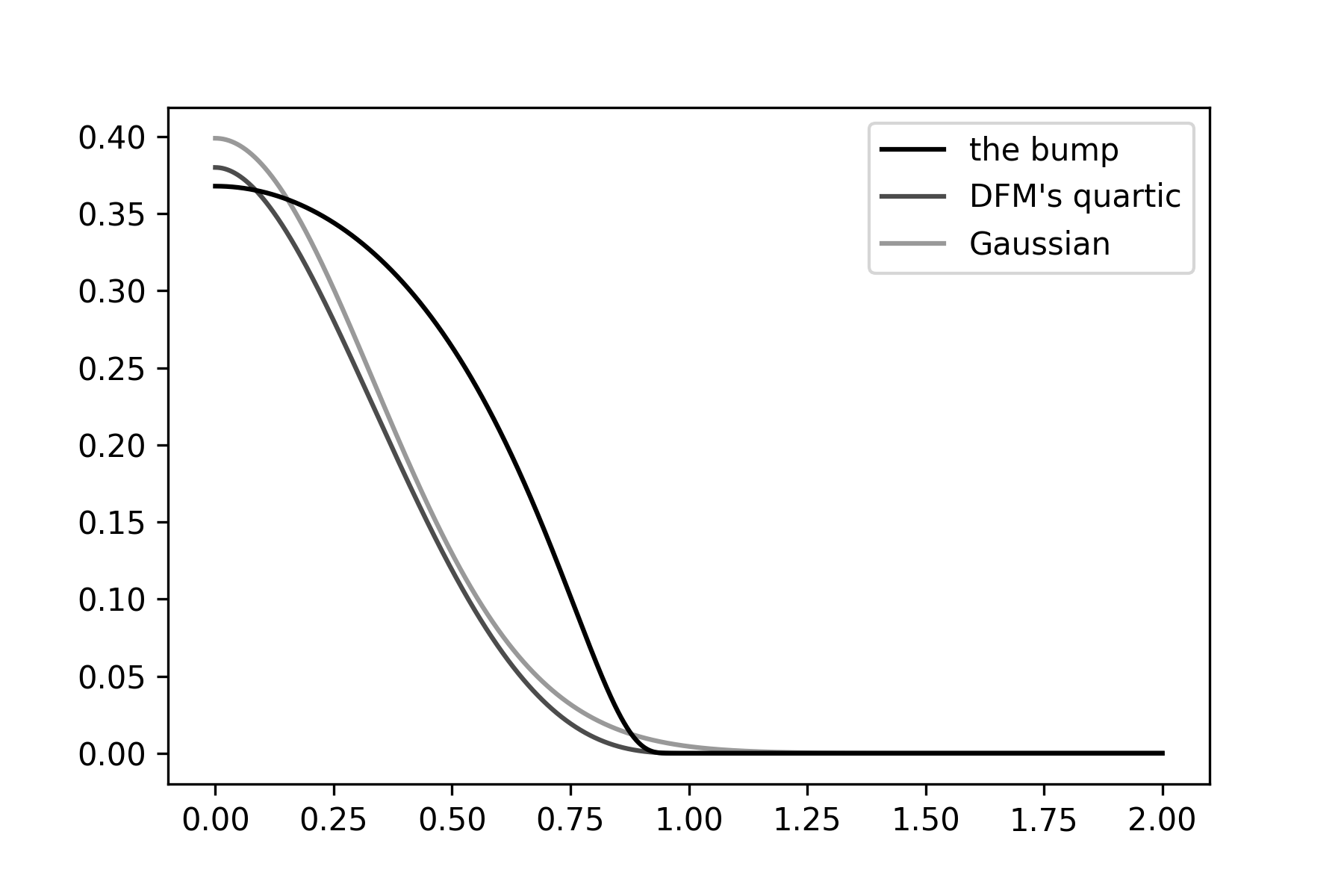
In group meeting today, I asked about twice-differentiable kernels with finite support. Finite support is good, because if a kernel has finite support, we can use kd-tree-like tricks to make the KDE much faster. Dan Foreman-Mackey (Flatiron) had a great idea: Just find the lowest-order polynomial (in radius) kernel that has zero slope at radius zero, and that goes to zero, zero slope, and zero second derivative at a radius of unity. I worked out the math for that over a beer and lo-and-behold there is a sweet quartic that does the trick (see figure).
Just as I was writing that code, Soledad Villar (JHU) texted me a link to the bump, which is differentiable to all orders. And it has a simple Fourier transform. It isn’t perfect though, because it has a lot of curvature where it goes to zero (see figure above). Time to implement something and see what happens.