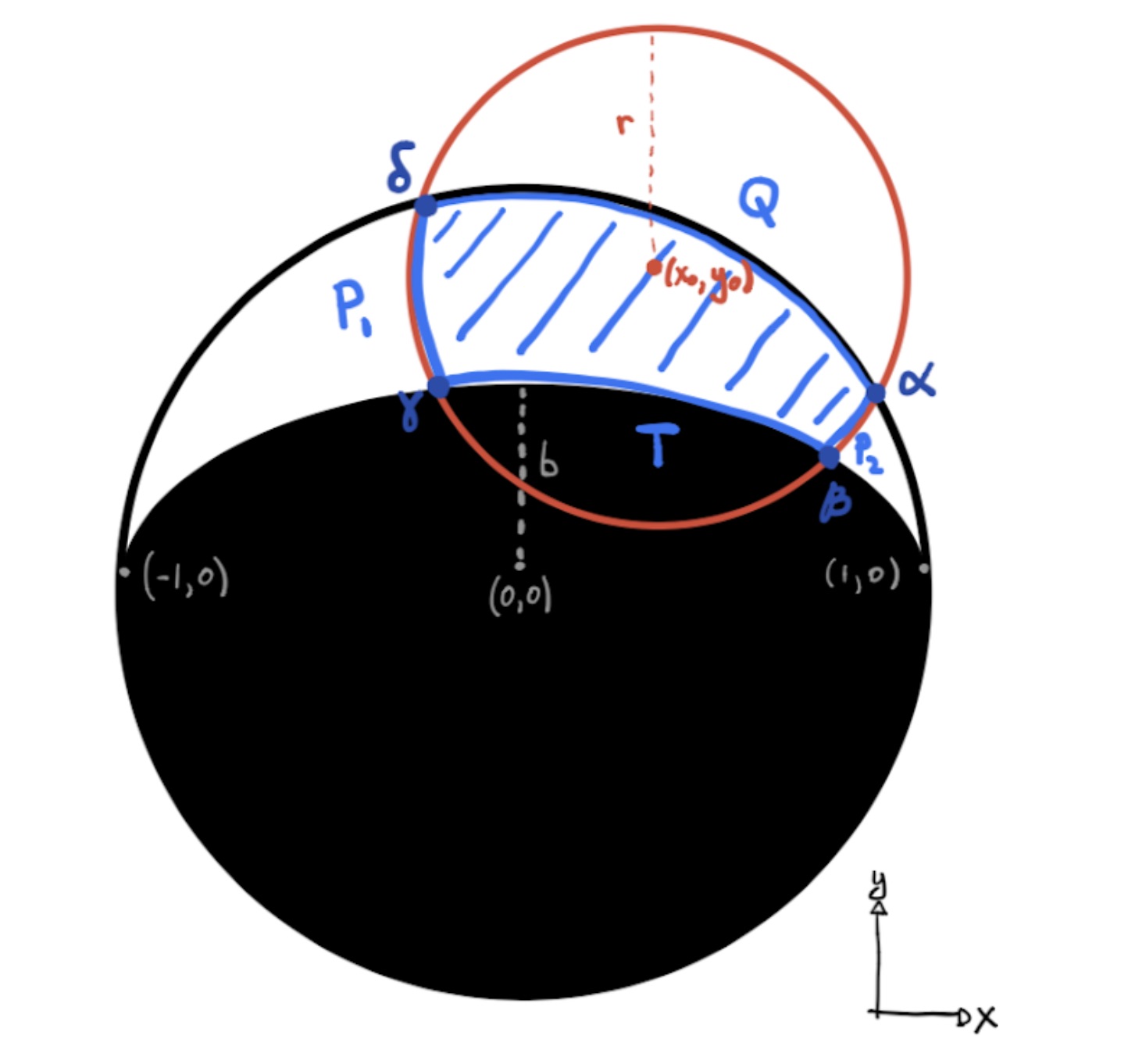
I’ve been working on the problem of computing occultation light curves of planets and moons in reflected light. This is an extension of my starry code to the case where the specific intensity on the surface of the body is zero beyond the day/night terminator. To compute the light curve of an occultation event like that shown in the figure, we need to integrate the specific intensity of the body over the portion of the dayside hemisphere that is facing the observer and not obscured by the occultor. It’s often easier to compute the occulted flux and subtract that from the total flux; the former is given by the integral over the region that is shaded in blue. In the original starry paper, I showed how this integral can be computed analytically in the case of thermal (emitted) light if we use Green’s theorem to transform it into a line integral along the boundary of the region. In the case of reflected light, the integral is still analytic, but harder because of the presence of the terminator. The tricky part is determining all of the integration paths (P1, Q, P2, and T) and endpoints (alpha, beta, gamma, delta). The terminator is always a segment of an ellipse, so we need to figure out how to programmatically identify all the points of intersection and traverse all of the segments that make up the boundary (of which there can be anywhere from two to five). This is proving to be tricky, since there are lots of different ways that two circles and an ellipse can intersect. But the end is in sight, and I hope to make this functionality available in starry in the next month or so.
This will hopefully have applications to modeling secondary eclipse (planet) light curves in the optical, occultations of Solar System bodies (such as mutual occultations of the Galilean moons), planet-planet occultations with JWST, and some day perhaps even exoplanet-exomoon occultations.