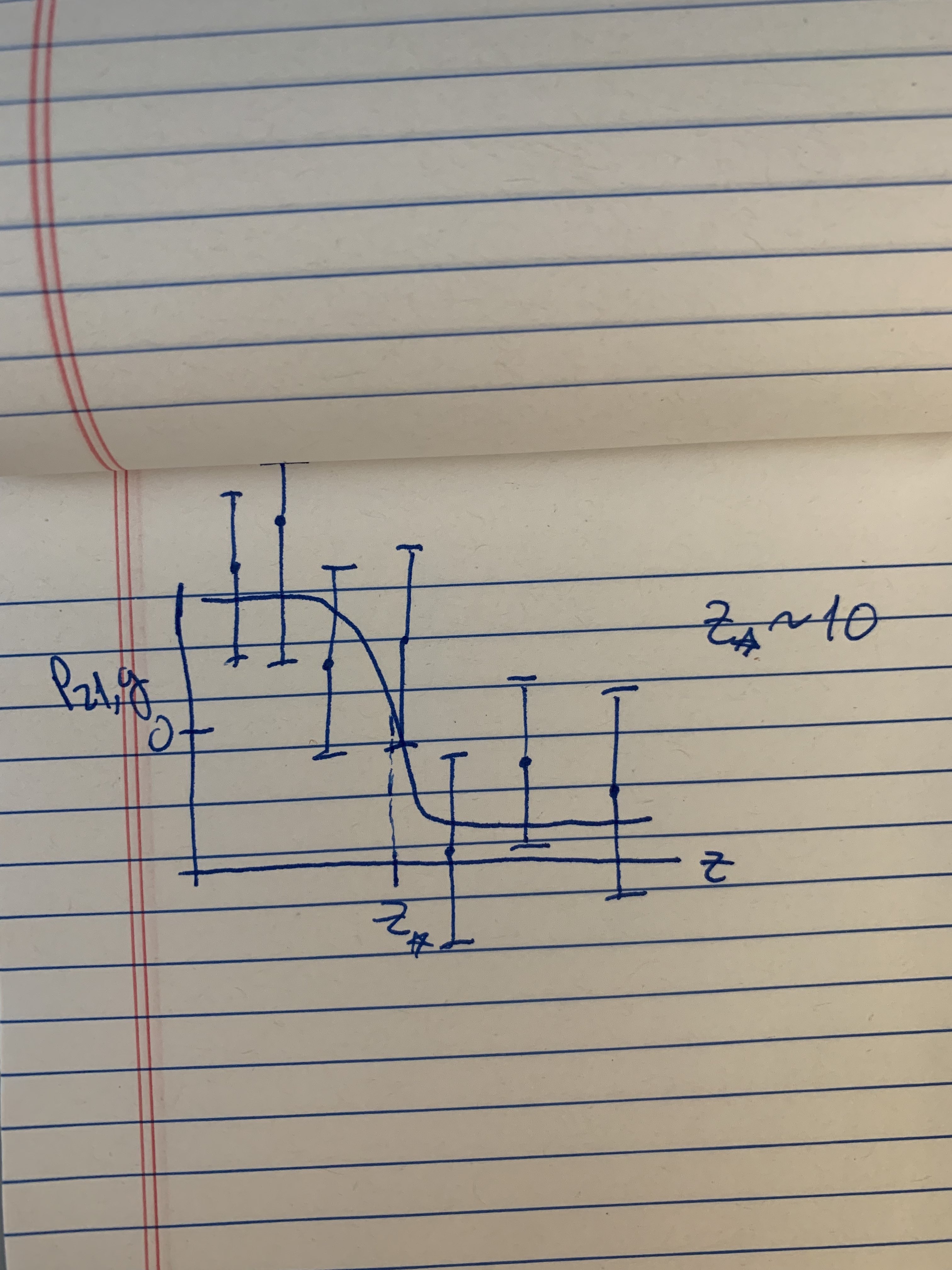
I’m working on a short reionization project where we want to figure out where a function crosses zero. I’ll spare the details of what this function (P21,g) is for the bottom of this post. But suffice it to say that the redshift where it transitions from being positive to negative (the “transition redshift”) is an interesting quantity. The plot shows a sketch of what the data might look like - where the function itself is not measured but the data still constrai
The issue is that the function we want to measure will be really hard to measure at these very high redshifts. But we’re not interested in actually measuring the value of the function – we just want to know where it crosses zero. From the data analysis side, these are two different questions. During the meeting, I discussed various ideas people have had that I’ve talked to. One simple way to proceed is just to fit some sort of reasonable function – like a logistic function – to the data, and sample over the parameters of the logistic function. Where the model crosses zero is then simply a parameter, and therefore one can back out a posterior distribution in a fairly straightforward way. We decided this will probably do just as well (or better) than some fancier methods.
Some more info about the function: During the early stages of reionization, a transition occurs where the 21cm signal and the density field go from being positively correlated on large scales to being negatively correlated. The sign can be measured in the cross-power spectrum between the two fields (the function, P21,g, spoken of earlier). In work in prep., we’ve shown (fairly easily) that the redshift at which this transition occurs (the “transition redshift”) is insensitive to the properties of whatever tracer you use of the density field (e.g., a galaxy survey or the properties of an intensity mapping field). The final piece of the project is simply showing that this transition redshift is measurable even though the cross-power spectrum isn’t.